跳转至

数组广播

信息

前置知识:

广播, broadcast, 是NumPy对不同形状的数据进行计算时采取的兼容措施.

目的

两个数组形状相同

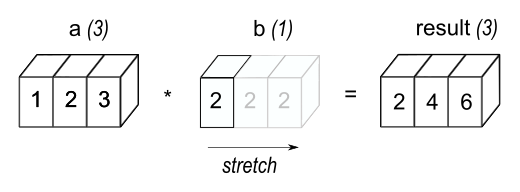
NumPy操作通常在成对的数组上逐元素进行. 在最简单的情况下, 这两个数组必须具有完全相同的形状(维度相同, 每一维度上的大小相同).

例子 
>>> import numpy as np
>>> a = np.array([1.0, 2.0, 3.0])
>>> b = np.array([2.0, 2.0, 2.0])
>>> a * b
array([2.,  4.,  6.])

两个数组形状不同

NumPy的广播机制在两个数组的形状满足一定要求时放松了对"具有完全相同的形状才能进行操作"的限制.

例子 
>>> import numpy as np
>>> a = np.array([1.0, 2.0, 3.0])
>>> b = 2.0
>>> a * b
array([2.,  4.,  6.])

这个结果和之前b是一个数组的时候相同. 我们可以想象标量b在算数运算时被延生成了一个和a形状相同的数组. 产生的数组中的元素是原标量b的副本. 这个延生的类比只是形式上的, 在实际内部, NumPy非常智能, 能够不创建延生数组而直接使用原始的标量b, 这会使广播占用较小的内存提高效率.

实际上, 这个例子中的运算比上个例子中的计算效率更高. 因为使用广播机制使得这个例子效率更高移动了更少的内存.

解释图:

广播规则

对于两个数组形状不同的情况, 要想使用广播, 这两个形状应当符合一定的要求.

笔记

我们将形状中的每一个维度称为该维度的大小.

例子 
>>> import numpy as np
>>> a = np.array([[1, 2, 3], [4, 5, 6]])
>>> a.shape
(2, 3)

形状(2, 3)中高维度的大小为2, 低纬度的大小为3.

NumPy会从右到左逐个维度地比较两个维度的大小. 这两个维度是兼容的如果:

  1. 相等
  2. 其中一个是1
注意
  • 两个数组的维度不一定要相同, 结果数组的维度和输入的两个数组中最大的维度相等, 结果数组中每个维度的大小和输入的两个数组中对应维度的最大大小相等. 缺失的维度大小被假设为1.
  • 如果上述地条件没有被满足, 则会抛出ValueError: operands could not be broadcase together错误, 表示无法进行广播, 即无法对两个数组进行操作.
例子

定义:

第一个数组的形状: 256 * 256 * 3
第二个数组的形状:             3

流程:

  1. 缺失的维度大小假设为1

    第一个数组的形状: 256 * 256 * 3
第二个数组的形状: 1   * 1   * 3

  2. 从右到左比较每一个维度

    1. 最右边的维度: 3和3, 相等, 兼容
    2. 中间的维度: 256和1, 其中一个是1, 兼容
    3. 最左边的维度: 256和1, 其中一个是1, 兼容

    这表示可以广播, 正确返回结果数组

  3. 结果数组的维度和输入的两个数组中最大的维度相等, 结果数组中每个维度的大小和输入的两个数组中对应维度的最大大小相等. 执行广播返回结果数组

    第一个数组的形状: 256 * 256 * 3
第二个数组的形状:             3
结果数组的形状:   256 * 256 * 3

定义:

第一个数组的形状: 8 * 1 * 6 * 1
第二个数组的形状:     7 * 1 * 5

流程:

  1. 缺失的维度大小假设为1

    第一个数组的形状: 8 * 1 * 6 * 1
第二个数组的形状: 1 * 7 * 1 * 5

  2. 从右到左比较每一个维度

    1. 最右边的维度: 1和5, 其中一个是1, 兼容
    2. 次右边的维度: 6和1, 其中一个是1, 兼容
    3. 次左边的维度: 1和7, 其中一个是1, 兼容
    4. 最左边的维度: 8和1, 其中一个是1, 兼容

    这表示可以广播, 正确返回结果数组

  3. 结果数组的维度和输入的两个数组中最大的维度相等, 结果数组中每个维度的大小和输入的两个数组中对应维度的最大大小相等. 执行广播返回结果数组

    第一个数组的形状: 8 * 1 * 6 * 1
第二个数组的形状: 1 * 7 * 1 * 5
结果数组的形状:   8 * 7 * 6 * 5

定义:

第一个数组的形状: 256 * 256 * 256
第二个数组的形状:             3

流程:

  1. 缺失的维度大小假设为1

    第一个数组的形状: 256 * 256 * 256
第二个数组的形状: 1   * 1   * 3

  2. 从右到左比较每一个维度

    1. 最右边的维度: 256和3, 不兼容
    2. 中间的维度: 256和1, 其中一个是1, 兼容
    3. 最左边的维度: 256和1, 其中一个是1, 兼容

    这表示不可以广播, 无法返回结果数组, 报错: ValueError: operands could not be broadcast together

定义:

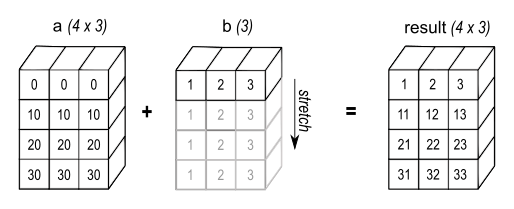
>>> a = np.array([[ 0.0,  0.0,  0.0],
...               [10.0, 10.0, 10.0],
...               [20.0, 20.0, 20.0],
...               [30.0, 30.0, 30.0]])
>>> b = np.array([1.0, 2.0, 3.0])
>>> a + b
array([[  1.,   2.,   3.],
        [11.,  12.,  13.],
        [21.,  22.,  23.],
        [31.,  32.,  33.]])
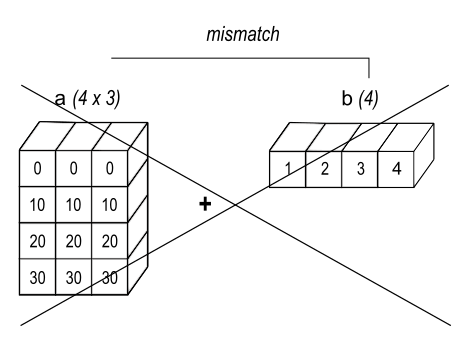
>>> b = np.array([1.0, 2.0, 3.0, 4.0])
>>> a + b
Traceback (most recent call last):
ValueError: operands could not be broadcast together with shapes (4,3) (4,)

解释:

  1. b = np.array([1.0, 2.0, 3.0])可广播:

  2. b = np.array([1.0, 2.0, 3.0, 4.0])不可广播:

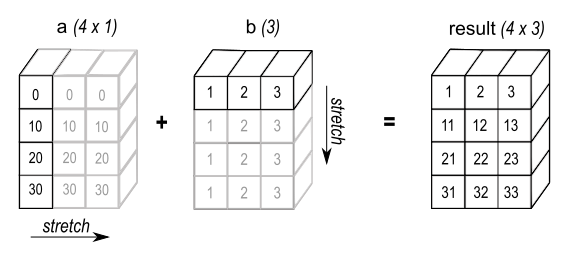
广播提供了一种简便的方法获取两个数组的外积/外加(或任何其他外部操作), 下面是两个一维行向量的外加操作:

>>> a = np.array([0.0, 10.0, 20.0, 30.0])
>>> b = np.array([1.0, 2.0, 3.0])
>>> a[:, np.newaxis] + b
array([[ 1.,   2.,   3.],
       [11.,  12.,  13.],
       [21.,  22.,  23.],
       [31.,  32.,  33.]])

关于a[:, np.newaxis]用于将一维行向量转为列向量, 详情见这里

原理图:

上述规则不但对两个数组适用, 如果一堆数组两两都符合上述规则, 则称这堆数组称为"可广播".

例子

假设有a, b, c, d四个数组, 它们的形状为:

假设它们的值为:

>>> a
array([[1],
       [2],
       [3],
       [4],
       [5]])
>>> b
array([[1, 2, 3, 4, 5, 6]])
>>> c
array([1, 2, 3, 4, 5, 6])
>>> d
1
根据上面的规则, 结果数组的形状为(5, 6). 详细解释广播的过程:

  • a的低维被广播, 变成:

    array([[1, 1, 1, 1, 1, 1],
       [2, 2, 2, 2, 2, 2],
       [3, 3, 3, 3, 3, 3],
       [4, 4, 4, 4, 4, 4],
       [5, 5, 5, 5, 5, 5]])

  • b的高维被广播, 变成:

    array([[1, 2, 3, 4, 5, 6],
       [1, 2, 3, 4, 5, 6],
       [1, 2, 3, 4, 5, 6],
       [1, 2, 3, 4, 5, 6],
       [1, 2, 3, 4, 5, 6]])

  • c缺失的维度的大小被假设为1, 所以情况和b类似, 变成:

    array([[1, 2, 3, 4, 5, 6],
        [1, 2, 3, 4, 5, 6],
        [1, 2, 3, 4, 5, 6],
        [1, 2, 3, 4, 5, 6],
        [1, 2, 3, 4, 5, 6]])

  • d缺失的维度的大小被假设为1, 重复单一的值, 变成:

    array([[1, 1, 1, 1, 1, 1],
       [1, 1, 1, 1, 1, 1],
       [1, 1, 1, 1, 1, 1],
       [1, 1, 1, 1, 1, 1],
       [1, 1, 1, 1, 1, 1]])

  1. Broadcasting—NumPy v2.0 Manual. (n.d.). Retrieved June 22, 2024, from https://numpy.org/doc/stable/user/basics.broadcasting.html ↩

  2. NumPy 广播(Broadcast) | 菜鸟教程. (n.d.). Retrieved June 22, 2024, from https://www.runoob.com/numpy/numpy-broadcast.html ↩